A stumbling block for the use of predictive cubic equations of state is that it is necessary to know something about the types of molecules that you are dealing with. For simple gas mixtures of light compoonents, a gas chromatograph mass spectrometer analysis from a lab can give you sufficient compositional breakdown to use these equations of state. But what about heavier hydrocarbon mixtures such as gas-condenate, volatile oil, or even crude oil itself? Here the C7+ components are not often well defined. Or at least there are two approaches used: (1) where the Katz-Firoozabadi single carbon number fractions are used to characterise the mixture, and (2) where an assay is performed separately that provides a lot of detail about the liquid composition, but is often not linked to the reservoir fluid composition.
The approach adopted by Pyrus is to use the assay results to guide the characterisation of a C7+ fraction where the MW, SG, SCN and PNA fractions are consistent. Whilst this is a somewhat simpler approach as it only considers a single C7+ fraction, it is very powerful and allows much better matching for a cubic equation of state to the laboratory results in comparison to a conventional cubic equation of state.
Once a plus fraction pseudo-component has been broken down into its constituent fractions of paraffins, naphthenes and aromatics, the door is opened to utilise methods that rely upon group contribution methods. These methods include cubic equations of state and estimation of viscosity.
Group Contribution Method for Enhanced Predictive Peng-Robinson Equation of State
Prediction of temperature-dependent binary interaction parameters (BIPs) with the Peng-Robinson equation of state for hydrocarbon fluids has led to improvements in vapour-liquid equilibrium calculations (Jaubert and Mutelet, 2004). The method introduced by Jaubert and Mutelet predicts the BIPs by breaking down components into molecular groups. Initially six groups were defined. These were CH3, CH2, CH, C, CH4 (methane) and C2H6 (ethane). This allowed prediction of BIPs to be used with the Peng-Robinson equation of state for normal and non-normal paraffins.
Since the initial method was published, several additional papers have been published which have expanded the number of groups, with the most recent also including compounds of relevance to carbon capture and sequestration (Xu et al, 2017). This allows prediction of BIPs to be expanded to compounds including naphthenes and aromatics.
A brief description of the equations used to predict BIPs can be found in an earlier post on cubic equations of state.
Advantages of EPPR78
The Enhanced Predictive Peng-Robinson (EPPR78) Equation of State is a powerful tool for modeling fluid properties, particularly in the field of petroleum engineering. When applied to simple mixtures of known hydrocarbon compounds, it has been reported that the predictive capabilities of the method are accurate and amongst the best performing equation of state models.
Equation of State models based on EPPR78 appear to require less tuning than other models to match experimental data. This improves the confidence in using results obtained using this method.
Challenges of Applying EPPR78 to Mixtures with C7+ Fraction
Group contribution methods such as EPPR78 have not found much application to real-world hydrocarbon mixtures. This is because of the difficulty associated with determining the groups that are present in a plus fraction. The plus fraction contains a wide number of different compounds, which makes it very hard to define the groups that are present in any plus fraction.
An approach to estimate the BIPs based on an estimation of the number of carbon atoms associated with paraffin, napthene and aromatic groups has been proposed (Xu et al, 2015). This approach is based on expressing the pseudo-component critical temperature (Tc), critical pressure (Pc) and acentric factor (ω) as functions of the number of carbon atoms for each group (NPAR, NNAP, NARO). The single carbon number for the cut is equal to NPAR + NNAP + NARO. Because three known properties can be expressed with three equations of three unknowns, the system can be solved.
Unfortunately the paper by Xu et al does not divulge much detail on how the group contributions for the different PNA content are best determined, but the paper does show that the performance of the characterised C7+ fraction versus a detailed reference description of the mixture is very good. An application of the methodology to a new cubic equation of state was described by Nasrifar and Rahmanian (2017). In their approach, it was assumed that all paraffins are represented by the CH2 or -CH2 group, all napthenes by the CH2, cyclic or -CH2- (R) group, and all aromatics by the CHaro or CH<( (R) group. This is evidently quite a simplistic assumption and it should not be hard to improve on the approach.
What this suggests is that if a reliable method of establishing the PNA content of a pseudo-component is used, a systematic approach to determining the group components for each of the paraffin, naphthene and aromatic fractions should allow EPPR78 to be used with pseudo-components.
Breaking Down the C7+ Fraction into Group Components
An alternative approach to determining the PNA fractions in a pseudo-component has already been described. Although this method was developed to describe the PNA content for different single carbon number fractionation cuts, it can equally be applied to a C7+ pseudo-component.
For any pseudo-component, it is possible to describe it using molecular weight, specific gravity, single carbon number and the PNA character. There is a relationship between all four characterisation parameters. Using these parameters, we can extend the approach to additionally define the group components that are associated with a pseudo-component. This is done by determining the typical average number of group components that are associated with each molecular type.
We will define the following parameters which are obtained from our pseudo-component characterisation:
- MW: molecular weight
- SG: specific gravity
- xp: paraffin fraction
- xn: naphthene fraction
- xa: aromatic fraction
- xma: mono-aromatic fraction
- xpa: poly-aromatic fraction
- PCN: Paraffin average carbon number
- NCN: Naphthene average carbon number
- ACN: Aromatic average carbon number
- SCN: Single carbon number (equivalent average carbon number for PNA fractions)
For each of our PNA fractions, we will determine group components for two varieties of that fraction: a simple representation and a more complex representation. For paraffins this is the difference between normal alkanes and branched alkanes. For naphthenes it is the difference between a single cyclic ring and multiple cyclic rings. For aromatics it is the difference between a single aromatic ring (mono-aromatic) and multiple aromatic rings (poly-aromatic). By applying the overall PNA fractions and the ratio of simple to complex compounds for each PNA fraction, the average number of group components for the pseudo-component can be determined. For any given fraction with a percentage N% of normal compounds, the total fraction of a group component is given by the following equation:
To determine the percentage of normal compounds (N%), we consider the specific gravity of the pseudo-component and compare this to the expected specific gravity for the normal paraffin with the same single carbon number for the paraffin fraction. More complex compounds tend to be smaller, and thus have a higher specific gravity.
/**
* Guess the overall percentage of complex versus simple compounds for paraffins. This is based on the overall
* specific gravity versus the normal paraffin specific gravity. It is a crude method that yields results that seem
* appropriate, but which are not based on any actual research or hard data. As such, it should be possible to
* improve the method if required.
*
* @param pcn paraffin carbon number for the distillation cut
* @param gamma specific gravity in liquid phase relative to water = 1.0
* @return educated guess for the overall percentage of complex compounds
*/
private static double complexPercentPN(double pcn, double gamma) {
double normal_paraffin_gamma = pcn / (1.14984 * pcn + 2.280525);
double model_gamma = getParaffinSgFromCarbonNum(pcn);
// Method assumes that the average paraffin sg vs pcn trend is approximately 10% complex compounds. Higher SG
// implies a larger percentage of complex compounds.
double cmplx_frac = ((gamma - normal_paraffin_gamma) / (model_gamma - normal_paraffin_gamma)) / 10.0;
return min(1.0, max(0.0, cmplx_frac)); // constrain to 0.0 to 1.0 range
}
Here, the method getParaffinSgFromCarbonNum obtains specific gravity of paraffinic components from the true average number of carbon atoms. It has been given in a previous blog post and establishes a trend for a mix of normal alkanes and branched alkanes versus the true average number of carbon atoms for those paraffin compounds.
Group Contributions for Paraffin Fraction
The paraffin fraction contains normal straight chain paraffins (n-alkanes) and non-normal paraffins which contain branches (branched alkanes). Equations have been derived to estimate the expected average fraction of groups associated with each of these paraffin types.
For normal paraffins with straight chains, such as n-Hexane shown below, there are only two groups: -CH3 and -CH2-. It is trivial to calculate the fraction for each of these groups given the average number of carbon atoms for the paraffin. There are always two -CH3 groups, with the remainder being -CH2- groups.
n-Hexane
The branched alkanes introduce two additional groups: >CH- and >C<. These can be seen in the molecular structures for 2-MethylPentane, 2,3-DiMethylButane and 2,2-DiMethylButane respectively:
2-MethylPentane
2,3-DiMethylButane
2,2-DiMethylButane
To calculate the number of groups for any given number of paraffin carbon atoms, it is necessary to make some assumptions. The strategy employed is to estimate the average fractions for the -CH3 and -CH groups. The -CH2 group can then be calculated by ensuring the number of hydrogen atoms for this PCN is consistent with that expected for a paraffin e.g., 2 × PCN + 2. Once the fractions for these three groups have been determined, the >CH< group can simply be calculated by ensuring that the fractions for all groups sum to unity.
For the -CH3 group we consider the minimum and maximum number of groups that might occur. The minimum is always three, where there is just a single branch e.g. 2-MethylPentane. This is given by the formula 3 / PCN. The maximum occurs when all available carbon atoms have a -CH3 group attached. The fraction is given by the formula FLOOR(2 + ((PCN - 2) / 2), 1) / PCN. Note the use of the floor function which rounds down to the nearest integer. This is required because for odd numbers of carbon atoms an orphan carbon atom remains along the spine of the molecule which cannot be paired with a -CH3 group. By calculating the minimum, maximum and average fractions for PCNs from 6 through to 40, a power trendline is fitted to the average fractions. This allows a generalised function to be applied.
For the >CH< group, the method requires some additional subtlety. This is because the number of groups can be zero, one (for our minimum -CH3 group molecules) up to (PCN - 2) / 2. To estimate the number of >CH< groups, we consider the maximum number of -CH3 groups case. Here, after ignoring the two end -CH3 groups, all other -CH3 groups are paired with a >CH< group. This is given by the formula FLOOR((PCN - 2) / 2, 1). Let us then consider that on average, only half of the maximum possible groups are actually >CH< groups. The fraction is thus given by the formula (FLOOR(FLOOR((PCN - 2) / 2, 1) / 2, 1)) / PCN. Again, a floor function is used to ensure an integer number of groups which creates a sawtooth effect when plotting against integer PCNs. As before, we plot these results for PCNs from 6 through to 40 and use a logarithmic trendline to allow a generalised application to any PCN.
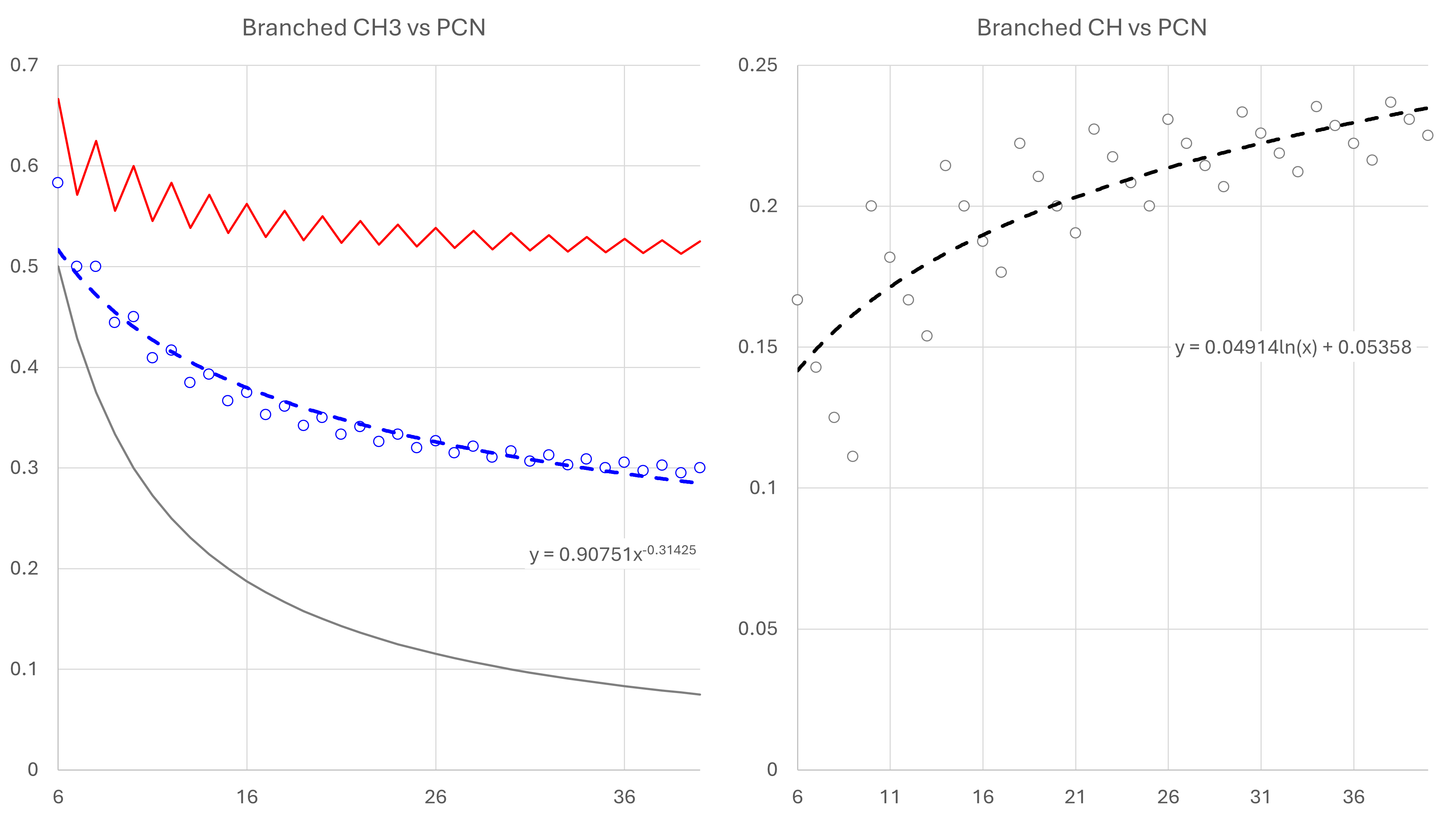
| Group | Normal Paraffin | Branched Paraffin |
|---|---|---|
| -CH3 | 2 / PCN | 0.90751 × PCN−0.31425 |
| -CH2- | 1 − -CH3 |
((-CH3normal × 3 + -CH2-normal × 2) − ((-CH3branched × 3) + >CH-branched) / 2 |
| >CH- | - | 0.04914 × log(PCN) + 0.05358 |
| >C< | - | 1 − (-CH3 + -CH2- + >CH-) |
Group Contributions for Naphthene Fraction
The naphthenes comprise ringed structures with two hydrogen atoms associated with each carbon atom in the ring. The simple compounds contain a single ring with one or more branches off the ring. Complex compounds can consist of two or more rings.
For our simple compounds, we base the group component contributions on the EthylCycloHexane structure. This is a single ring with an ethyl branch (-CH2- and -CH3 groups). We can estimate the groups for integer numbers of carbon atoms easily based on this structure. For NCN < 8 we need to consider the special cases for NCN = 7 and NCN = 6. For NCN = 7 we change the ethyl branch to a methyl branch (single -CH3 group), thus losing a -CH2- group in comparison to NCN = 8. For NCN = 6 we have a CycloHexane ring, which loses the -CH3, -CH2- and >CH- (R) groups, and gains a -CH2- (R) group. For NCN > 9 we can add -CH2- groups. This is essentially a normal paraffin with a CycloHexane ring attached. The calculations that result from this logic are shown in the table below for the “Simple” column.
EthylCycloHexane
For our complex compounds we can look at how the groups evolve as the napthenic carbon number increases. As we increase the number of atoms above those in a single ring we start to add methyl (one carbon), ethyl (two carbons), propyl (three carbons) and butyl (four carbons) branches. With four carbon atoms we can also close a second ring. This sets up a pattern for the number of groups associated with each NCN. Whilst this is just for cyclohexane rings, and ignores the possibility of other cycloalkane ring structures, it should provide a reasonable estimate of the relative importance of different groups.
| Molecule | NCN | -CH3 | -CH2- | >CH- | >C< | -CH2- (R) | >CH- (R) | >C< (R) |
|---|---|---|---|---|---|---|---|---|
| CycloHexane | 6 | - | - | - | - | 6 | - | - |
| MethylCycloHexane | 7 | 1 | - | - | - | 5 | 1 | - |
| EthylCycloHexane | 8 | 1 | 1 | - | - | 5 | 1 | - |
| 1,1-DimethylCycloHexane | 8 | 2 | - | - | - | 5 | - | 1 |
| PropylCycloHexane | 9 | 1 | 2 | - | - | 5 | 1 | - |
| IsopropylCycloHexane | 9 | 2 | - | 1 | - | 5 | 1 | - |
| ButylCycloHexane | 10 | 1 | 3 | - | - | 5 | 1 | - |
| IsobutylCycloHexane | 10 | 2 | 1 | 1 | - | 5 | 1 | - |
| TertbutylCycloHexane | 10 | 3 | - | - | 1 | 5 | 1 | - |
| DecaHydroNaphthalene | 10 | - | - | - | - | 8 | 2 | - |
| 1-MethylDecaHydroNaphthalene | 11 | 1 | - | - | - | 7 | 3 | - |
Using a similar approach to that used with the branched paraffins, we create equations that approximate the group component fractional amounts shown in the table. These equations are shown in the table below:
| Group / Variable | Simple Naphthene | Complex Naphthene |
|---|---|---|
| ncyc | - | QUOTIENT(NCN - 7, 4) + 1 |
| ncbranch | - | MAX(0, NCN - ((n_cyc - 1) * 4 + 6)) |
| -CH3 | (1 - (-CH2- + -CH2- (R))) / 2 |
(0.075 × nc_branch^2 − 0.045 × nc_branch + 0.975) / NCN |
| -CH2- | (NCN > 7) ? NCN - 7 / NCN : 0 | MAX(0, ((NCN - 1) - ((n_cyc - 1) * 4 + 6)) / 2.7) / NCN |
| >CH- | - | MAX(0, ((NCN - 1) - ((n_cyc - 1) * 4 + 6)) / 5.5) / NCN |
| >C< | - | MAX(0, ((NCN - 1) - ((n_cyc - 1) * 4 + 6)) / 12) / NCN |
| -CH2- (R) | (NCN > 6) ? 5 / NCN : 1 | ((n_cyc - 1) * 2 + 5) / NCN |
| >CH- (R) | (1 - (-CH2- + -CH2- (R))) / 2 |
-CH2- (R) - (nc_branch / 10 + 4) / NCN |
| >C< (R) | - | MAX(0, 1 − (-CH3 + -CH2- + >CH- + >C< + -CH2- (R) + >CH- (R))) |
Note: Table uses ternary conditional operator to express logic. The equations for all group components may not add to unity, so fractions must be normalised to 1.0 after calculation.
Group Contributions for Aromatic Fraction
The aromatics comprise ringed structures with two hydrogen atoms associated with each carbon atom in the ring. The simple compounds contain a single ring with one or more branches off the ring. Complex compounds can consist of two or more rings.
EthylBenzene
| Molecule | ACN | -CH3 | -CH2- | >CH- | >C< | )>CH (R) | )>C- (R) | )>C<( (R) |
|---|---|---|---|---|---|---|---|---|
| Benzene | 6 | - | - | - | - | 6 | - | - |
| MethylBenzene | 7 | 1 | - | - | - | 5 | 1 | - |
| EthylBenzene | 8 | 1 | 1 | - | - | 5 | 1 | - |
| 1,1-DimethylBenzene | 8 | 2 | - | - | - | 5 | - | 1 |
| PropylBenzene | 9 | 1 | 2 | - | - | 5 | 1 | - |
| IsopropylBenzene | 9 | 2 | - | 1 | - | 5 | 1 | - |
| ButylBenzene | 10 | 1 | 3 | - | - | 5 | 1 | - |
| IsobutylBenzene | 10 | 2 | 1 | 1 | - | 5 | 1 | - |
| TertbutylBenzene | 10 | 3 | - | - | 1 | 5 | 1 | - |
| Naphthalene | 10 | - | - | - | - | 8 | 2 | - |
| 1-MethylNaphthalene | 11 | 1 | - | - | - | 7 | 3 | - |
Again we use a similar approach to that used with the branched paraffins. Equations are created that approximate the group component fractional amounts shown in the table. These equations are shown in the table below:
| Group | Mono Aromatic | Poly Aromatic |
|---|---|---|
| naro | - | QUOTIENT(ACN - 7, 4) + 1 |
| acbranch | - | MAX(0, ACN - ((n_aro - 1) * 4 + 6)) |
| -CH3 | (1 - (-CH2- + CH<( (R))) / 2 |
(0.075 × ac_branch^2 − 0.045 × ac_branch + 0.975) / ACN |
| -CH2- | (ACN > 7) ? ACN - 7 / ACN : 0 | MAX(0, ACN - ((n_aro - 1) * 4 + 6)) |
| >CH- | - | MAX(0, ((ACN - 1) - ((n_aro - 1) * 4 + 6)) / 5.5) / ACN |
| >C< | - | MAX(0, ((ACN - 1) - ((n_aro - 1) * 4 + 6)) / 12) / ACN |
| )>CH (R) | (ACN > 6) ? 5 / ACN : 1 | ((n_aro - 1) * 2 + 5) / ACN |
| )>C- (R) | (1 - (-CH2- + CH<( (R))) / 2 |
CH<( (R) - (ac_branch / 10 + 4) / ACN |
| )>C<( (R) | - | MAX(0, 1 − (-CH3 + -CH2- + >CH- + >C< + CH<( (R) + -C<( (R))) |
Note: Table uses ternary conditional operator to express logic. The equations for all group components may not add to unity, so fractions must be normalised to 1.0 after calculation.
Combining PNA Groups
Once the group fractions for each of the paraffin, naphthene and aromatic fractions have been determined, the overall total group contributions can be calculated from the PNA fractions. This is a simple linear combination for each group component:
A worked example based on the Katz-Firoozabadi C9 fraction is shown. This Katz-Firoozabadi has the following properties:
- MW: 121.0 g/mole
- SG: 0.768× relative to water
Properties for other variables are derived from these values in accordance with the approach used for C7+ characterisation but with updated methodology for determining PNA fractions. Boiling point is determined using the Soreide (1989) correlation. This allows Watson factor to be calculated from boiling point and API gravity (obtained from specific gravity). Critical temperature, pressure and volume can be determined from correlations such as Riazi-Adwani and Twu. Acentric factor is determined from the Kesler-Lee correlation. We can determine PNA fractions based on these values, and then from the MW, SG and PNA, the average number of carbon atoms can be calculated. Note that the single carbon number (SCN) which is the normal paraffin associated with the true boiling point is different to the average number of carbon atoms, and can be determined from the boiling point.
For the Katz-Firoozabadi C9 fraction the following parameters are obtained through use of the characterisation procedure:
- PNA fractions: Paraffin = 63.13%, Naphthene = 12.95%, Aromatic = 23.91%
- Complex ratio: Normal paraffin/naphthene = 62.37%
- Aromatic ratio: Mono-aromatic fraction = 98.62%
- Single carbon number (SCN): 9
- Paraffin carbon number (PCN): 9.083
- Naphthene carbon number (NCN): 8.314
- Aromatic carbon number (ACN): 7.747
- Average carbon number (nC): 8.662
Using the formulae described above, we obtain the following group components for the C9 pseudo-component.
| Group | Normal P | Branched P | Paraffin | Simple N | Complex N | Naphthene | Mono A | Poly A | Aromatic | Overall |
|---|---|---|---|---|---|---|---|---|---|---|
| -CH3 | 0.2202 | 0.4537 | 0.3081 | 0.1203 | 0.1530 | 0.1326 | 0.1292 | 0.1452 | 0.1295 | 0.2426 |
| -CH2- | 0.7798 | 0.3486 | 0.6175 | 0.1580 | 0.0585 | 0.1206 | 0.0953 | 0.0353 | 0.0945 | 0.4281 |
| >CH- | - | 0.1620 | 0.0610 | - | 0.0287 | 0.0108 | - | 0.0173 | 0.0002 | 0.0399 |
| >C< | - | 0.0357 | 0.0134 | - | 0.0132 | 0.0050 | - | 0.0079 | 0.0001 | 0.0092 |
| )>CH (R) | - | - | - | - | - | - | 0.6462 | 0.6462 | 0.6462 | 0.1545 |
| )>C- (R) | - | - | - | - | - | - | 0.1292 | 0.1068 | 0.1289 | 0.0308 |
| )>C<( (R) | - | - | - | - | - | - | - | 0.0413 | 0.0006 | 0.0001 |
| -CH2- (R) | - | - | - | - | - | 0.6014 | - | - | - | 0.0779 |
| >CH- (R) | - | - | - | - | - | 0.1098 | - | - | - | 0.0142 |
| >C< (R) | - | - | - | - | - | 0.0198 | - | - | - | 0.0026 |
It can be seen that -CH2-, )>CH (R) and -CH2- (R) groups are the main groups for the paraffins, naphthenes and aromatics, but -CH3 is also predominant. Other groups are very minor contributions only.
A code snippet from Pyrus used to implement the described equations is as follows:
/**
* The PPR78 equation of state requires that the ratio of group components for each component are defined. This is
* challenging when dealing with a pseudo as the theoretical structures possible run into the many thousands.
* Despite this we can generalise the nature of the components, and split the pseudo into three main types of
* hydrocarbon e.g. paraffin, naphthene (single saturated cyclic ring) and aromatics (single ring). Paraffins and
* naphthenes have been modelled with different degrees of branching complexity.
*
* @param pna proportion of pseudo-component describing PNA fractions as an array [p, n, a, pa, ma] where p
* comprises straight chain or branched paraffins, n is the proportion comprising cyclic (saturated) ring as major
* structure, a is the proportion of aromatic (single ring), pa is the proportion comprising poly-aromatic and ma is
* the proportion comprising mono-aromatic
* @param normal proportion of compounds that have simple chains
*/
private void setPNAGroups(double[] pna, double normal) {
x_p = pna[0];
x_n = pna[1];
x_a = pna[2];
x_pa = pna[3];
x_ma = pna[4];
/*
* First we get the equivalent single carbon number from which all group component ratios are derived. This is
* based on modelling of group components for common paraffins, napthenes and aromatics, and then tweaking the
* SCN found so that the molecular mass calculated for Katz-Firoozabdi SCN components is reasonable using this
* method. The adjustment to SCN is only for the calculation of group component fractions.
*/
double pcn = estimatePCN(mass, x_p, x_a); // mass is molecular weight in g/mole
double ncn = getNaphtheneCarbonNumFromPCN(pcn);
double acn = getAromaticCarbonNumFromPCN(pcn);
/*
* Calculate the paraffin group component ratios
*/
double[] p_ch3 = new double[3];
double[] p_ch2 = new double[3];
double[] p_ch = new double[3];
double[] p_c = new double[3];
// Simple alkanes with length of chain dependent on average SCN
p_ch3[0] = 2.0 / pcn;
p_ch2[0] = 1.0 - p_ch3[0];
// Branched paraffins with increased branching for higher SCN
p_ch3[1] = 0.90751 * pow(pcn, -0.31425);
p_ch[1] = 0.04914 * log(pcn) + 0.05358;
p_ch2[1] = ((p_ch3[0] * 3.0 + p_ch2[0] * 2.0) - (p_ch3[1] * 3.0 + p_ch[1])) / 2.0;
p_c[1] = 1.0 - (p_ch3[1] + p_ch2[1] + p_ch[1]);
double p_grpsum = p_ch3[1] + p_ch2[1] + p_ch[1] + p_c[1];
// Average fractions for each group contribution from paraffins
p_ch3[2] = p_ch3[0] * normal + (p_ch3[1] / p_grpsum) * (1.0 - normal);
p_ch2[2] = p_ch2[0] * normal + (p_ch2[1] / p_grpsum) * (1.0 - normal);
p_ch[2] = p_ch[0] * normal + (p_ch[1] / p_grpsum) * (1.0 - normal);
p_c[2] = p_c[0] * normal + (p_c[1] / p_grpsum) * (1.0 - normal);
/*
* Calculate the naphthene group component ratios
*/
double[] n_ch3 = new double[3];
double[] n_ch2 = new double[3];
double[] n_ch = new double[3];
double[] n_c = new double[3];
double[] n_ch2cyc = new double[3];
double[] n_chcyc = new double[3];
double[] n_ccyc = new double[3];
int n_cycring = ((int) ncn - 7) / 4 + 1;
double nc_branch = max(0.0, ncn - ((n_cycring - 1.0) * 4.0 + 6.0));
// Single cyclic ring with single branch
n_ch2[0] = (ncn > 7) ? (ncn - 7.0) / ncn : 0.0;
n_ch2cyc[0] = (ncn > 6) ? 5.0 / ncn : 1.0;
n_ch3[0] = (1.0 - (n_ch2[0] + n_ch2cyc[0])) / 2.0;
n_chcyc[0] = n_ch3[0];
// Complex cyclic rings with branches
n_ch3[1] = (0.075 * pow(nc_branch, 2.0) - 0.045 * nc_branch + 0.975) / ncn;
n_ch2[1] = max(0.0, ((ncn - 1.0) - ((n_cycring - 1.0) * 4.0 + 6.0)) / 2.7) / ncn;
n_ch[1] = max(0.0, ((ncn - 1.0) - ((n_cycring - 1.0) * 4.0 + 6.0)) / 5.5) / ncn;
n_c[1] = max(0.0, ((ncn - 1.0) - ((n_cycring - 1.0) * 4.0 + 6.0)) / 12.0) / ncn;
n_ch2cyc[1] = ((n_cycring - 1.0) * 2.0 + 5.0) / ncn;
n_chcyc[1] = n_ch2cyc[1] - (nc_branch / 10.0 + 4.0) / ncn;
n_ccyc[1] = max(0.0, 1.0 - (n_ch3[1] + n_ch2[1] + n_ch[1] + n_c[1] + n_ch2cyc[1] + n_chcyc[1]));
double n_grpsum = n_ch3[1] + n_ch2[1] + n_ch[1] + n_c[1] + n_ch2cyc[1] + n_chcyc[1] + n_ccyc[1];
// Average fractions for each group contribution from naphthenes
n_ch3[2] = n_ch3[0] * normal + (n_ch3[1] / n_grpsum) * (1.0 - normal);
n_ch2[2] = n_ch2[0] * normal + (n_ch2[1] / n_grpsum) * (1.0 - normal);
n_ch[2] = n_ch[0] * normal + (n_ch[1] / n_grpsum) * (1.0 - normal);
n_c[2] = n_c[0] * normal + (n_c[1] / n_grpsum) * (1.0 - normal);
n_ch2cyc[2] = n_ch2cyc[0] * normal + (n_ch2cyc[1] / n_grpsum) * (1.0 - normal);
n_chcyc[2] = n_chcyc[0] * normal + (n_chcyc[1] / n_grpsum) * (1.0 - normal);
n_ccyc[2] = n_ccyc[0] * normal + (n_ccyc[1] / n_grpsum) * (1.0 - normal);
/*
* Calculate the aromatic group component ratios
*/
double[] a_ch3 = new double[3];
double[] a_ch2 = new double[3];
double[] a_ch = new double[3];
double[] a_c = new double[3];
double[] a_charo = new double[3];
double[] a_caro = new double[3];
double[] a_cfused = new double[3];
int a_aroring = ((int) acn - 7) / 4 + 1;
double ac_branch = max(0.0, acn - ((a_aroring - 1.0) * 4.0 + 6.0));
// Single aromatic ring with single branch
a_ch2[0] = (acn > 7) ? (acn - 7.0) / acn : 0.0;
a_charo[0] = (acn > 6) ? 5.0 / acn : 1.0;
a_ch3[0] = (1.0 - (a_ch2[0] + a_charo[0])) / 2.0;
a_caro[0] = a_ch3[0];
// Poly-aromatic rings with branches
a_ch3[1] = (0.075 * pow(ac_branch, 2.0) - 0.045 * ac_branch + 0.975) / acn;
a_ch2[1] = max(0.0, ((acn - 1.0) - ((a_aroring - 1.0) * 4.0 + 6.0)) / 2.7) / acn;
a_ch[1] = max(0.0, ((acn - 1.0) - ((a_aroring - 1.0) * 4.0 + 6.0)) / 5.5) / acn;
a_c[1] = max(0.0, ((acn - 1.0) - ((a_aroring - 1.0) * 4.0 + 6.0)) / 12.0) / acn;
a_charo[1] = ((a_aroring - 1.0) * 2.0 + 5.0) / acn;
a_caro[1] = a_charo[1] - (ac_branch / 10.0 + 4.0) / acn;
a_cfused[1] = max(0.0, 1.0 - (a_ch3[1] + a_ch2[1] + a_ch[1] + a_c[1] + a_charo[1] + a_caro[1]));
double a_grpsum = a_ch3[1] + a_ch2[1] + a_ch[1] + a_c[1] + a_charo[1] + a_caro[1] + a_cfused[1];
double monofrac = (x_ma + x_pa) > 0.0 ? x_ma / (x_ma + x_pa) : 1.0;
// Average fractions for each group contribution from aromatics
a_ch3[2] = a_ch3[0] * monofrac + (a_ch3[1] / a_grpsum) * (1.0 - monofrac);
a_ch2[2] = a_ch2[0] * monofrac + (a_ch2[1] / a_grpsum) * (1.0 - monofrac);
a_ch[2] = a_ch[0] * monofrac + (a_ch[1] / a_grpsum) * (1.0 - monofrac);
a_c[2] = a_c[0] * monofrac + (a_c[1] / a_grpsum) * (1.0 - monofrac);
a_charo[2] = a_charo[0] * monofrac + (a_charo[1] / a_grpsum) * (1.0 - monofrac);
a_caro[2] = a_caro[0] * monofrac + (a_caro[1] / a_grpsum) * (1.0 - monofrac);
a_cfused[2] = a_cfused[0] * monofrac + (a_cfused[1] / a_grpsum) * (1.0 - monofrac);
// Combine the paraffin, naphthene and aromatic group components together
double ch3 = x_p * p_ch3[2] + x_n * n_ch3[2] + x_a * a_ch3[2];
double ch2 = x_p * p_ch2[2] + x_n * n_ch2[2] + x_a * a_ch2[2];
double ch = x_p * p_ch[2] + x_n * n_ch[2] + x_a * a_ch[2];
double c = x_p * p_c[2] + x_n * n_c[2] + x_a * a_c[2];
double charo = x_a * a_charo[2];
double caro = x_a * a_caro[2];
double cfused = x_a * a_cfused[2];
double ch2cyc = x_n * n_ch2cyc[2];
double chcyc = x_n * n_chcyc[2];
double ccyc = x_n * n_ccyc[2];
// Set the groups using the values obtained. Array here is specific for Pyrus but other structures are possible.
groups = new double[]{ch3, ch2, ch, c, 0.0, 0.0, charo, caro, cfused, ch2cyc, chcyc, ccyc, 0.0, 0.0, 0.0, 0.0,
0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0};
}
Application of EPPR78
Equinor’s Volve dataset is freely available and provides the opportunity to test the performance of the EPPR78 equation of state combined with the BIPs calculated for a C7+ component in accordance with the approach outlined in this post.
The composition of bottom hole sample #1 (BHS #1) is as follows:
| Component | Fraction |
|---|---|
| CO2 | 0.04938 |
| N2 | 0.00459 |
| CH4 | 0.43428 |
| C2H6 | 0.06057 |
| C3H8 | 0.0526 |
| IC4 | 0.0069 |
| NC4 | 0.02658 |
| IC5 | 0.00921 |
| NC5 | 0.01511 |
| C6 | 0.02085 |
| C7+ | 0.31993 |
| C+MW | 244.3608102 |
| C+GAMMA | 0.820667077 |
Here the C+MW and C+GAMMA are the molecular weight and specific gravity of the C7+ fraction respectively.
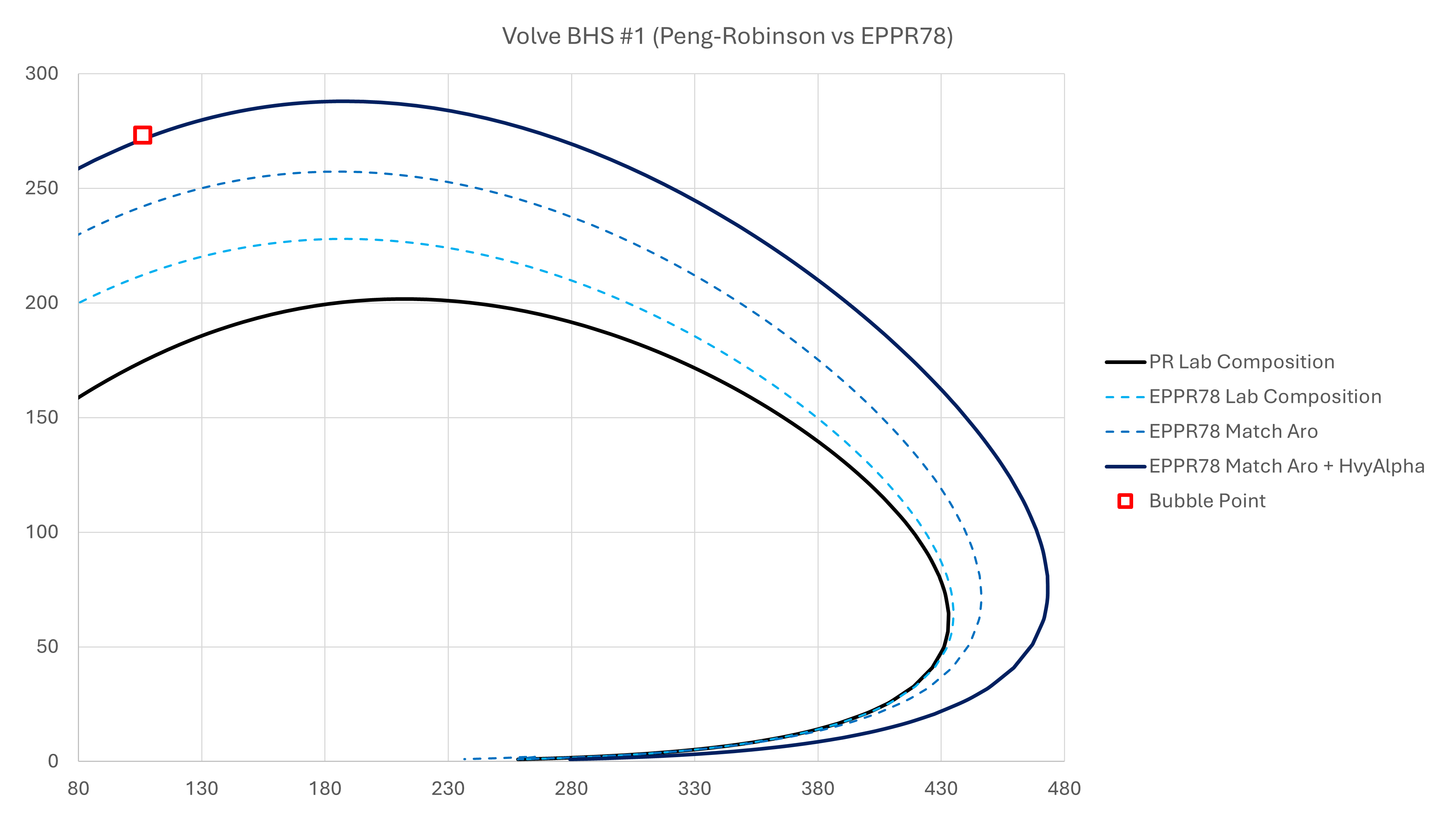
The composition can be used with the Peng-Robinson cubic equation of state. The resultant phase envelope does not match the laboratory-measured bubble point. By switching to the EPPR78 equation of state, there is an improvement in the bubble point prediction. However, this is still not a good match. The distillation data from the Volve dataset shows that the aromatic content is actually higher than that implied by the MW and SG for the C7+ fraction. Given the the mass chromotograph is more likely to measure the weight% for the C7+ fraction more accurately than the density (which is inferred from a Katz-Firboozabadi calcuation/assumption), we can adjust the PNA to match the measured aromatic content of 35.2%. This increases the specific gravity to 0.8601, and leads to a closer match with the measured bubble point.
Ideally, no tuning for an equation of state would be necessary with a perfect model. However, this is not yet reasonable, and many compositions require a small amount of tuning. By using the EPPR78 and adjusting the C7+ specific gravity to match the PNA fractions, the amount of tuning required in comparison to the vanilla Peng-Robinson equation of state is greatly reduced.
In this case we have simply increased the heavy fraction α by 1.08×. This leads to a close match to the measured bubble point. A comparison of the different phase envelopes obtained using the Pyrus Suite and workflow described are shown in the figure below:
References
- Jaubert, J. and Mutelet, F. 2004. VLE Predictions with the Peng-Robinson Equation of State and Temperature Dependent kij Calculated Through a Group Contribution Method. Fluid Phase Equilibria 224 (2): 2855-304. https://doi.org/10.1016/j.fluid.2004.06.059
- Nasrifar, K. and Rahmanian, N. 2018. Equations of State with Group Contribution Binary Interaction Parameters for Calculation of Two-Phase Envelopes for Synthetic and Real Natural Gas Mixtures with Heavy Fractions. Oil & Gas Science & Technology 73 (7). https://doi.org/10.2516/ogst/2017044
- Xu, X., Jaubert, J., Privat, R., Duchet-Suchaux, P., Braña-Mulero, F. 2015. Predicting Binary-Interaction Parameters of Cubic Equations of State for Petroleum Fluids Containing Pseudo-Components. Ind. Eng. Chem. Res. 54 (10): 2816-2824. https://doi.org/10.1021/ie504920g
- Xu, X., Lasala, S., Privat, R., Jaubert, J. 2017. E-PPR78: A Proper Cubic EoS for Modelling Fluids Involved in the Design and Operation of Carbon Dioxide Capture and Storage (CCS) Processes. International Journal of Greenhouse Gas Control 56: 123-154. https://doi.org/10.1016/j.ijggc.2016.11.015