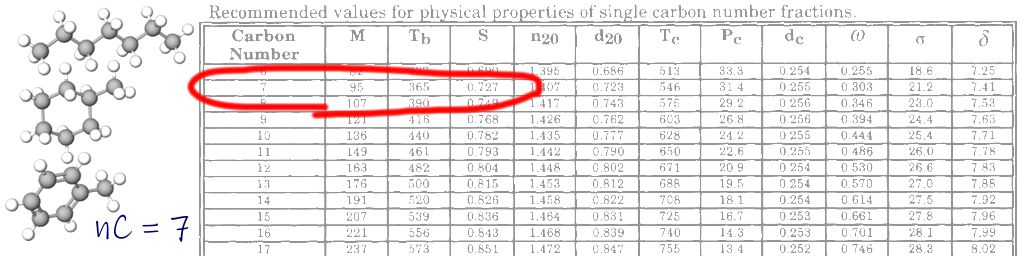
To use any equation of state that relies on group contribution methods, a reasonably accurate and robust method to estimate the fraction of paraffins, naphthenes and aromatics (PNA) is required. It is from this knowledge of the different molecular compounds contained within a fraction that estimates of the number of different groups can be made. Estimating the PNA fractions is a critical step.
There exists a relationship between the molecular weight (MW), specific gravity (SG), PNA content and the average number of carbon atoms per molecule for any hydrocarbon fraction. My previous approach to the problem assumed that the single carbon number (SCN) for a distillation cut was the same for paraffins, naphthenes and aromatics, and that knowledge of this number could be used to calculate molecular weight from PNA and SCN alone via knowledge of the typical molecular structures for the different hydrocarbon types. This was a very simplistic assumption.
Because MW, SG, PNA and SCN are all related, renewed focus into understanding what the SCN represents has allowed a more comprehensive method that relates all four properties to be created. The method has been ‘tuned’ using the Volve PVT dataset which has been made publically available by Equinor, and shows a good agreement between the modelled and measured values.
Improving Riazi-Daubert Correlations
An earlier post on C7+ characterisation showed a method that I had been using to estimate the relative fractions of paraffin, naphthene and aromatics in a particular lumped pseudo-component (or distillation cut in the case of the Katz-Firoozabadi single carbon number fractions). The method used was by no means novel, and relied upon correlations published by Riazi and Daubert (1986). The Riazi-Daubert approach was used by Riazi and Al-Sahhaf (1996) when predicting properties of hydrocarbon fractions from C6 to C50, although they only published PNA for compounds up to C22.
The problem with using the Riazi-Daubert correlations directly is that there is an evident discontinuity that can be seen between C14 to C15 in the graph on the left in Figure 1. Originally I had dismissed this as an artefact of the Katz-Firoozabadi fractions as their paper states that they had combined three datasets with C5 to C15, C16 to C22, and C22 to C45 in order to create a continuous sequence of single carbon number cuts. Upon checking the published data in the original Riazi and Daubert paper, it was apparent that the dataset used to establish the regressions used for the heavy hydrocarbons was notably different to that used for the light hydrocarbons. The discontinuity was a real artefact that arises from the datasets used.
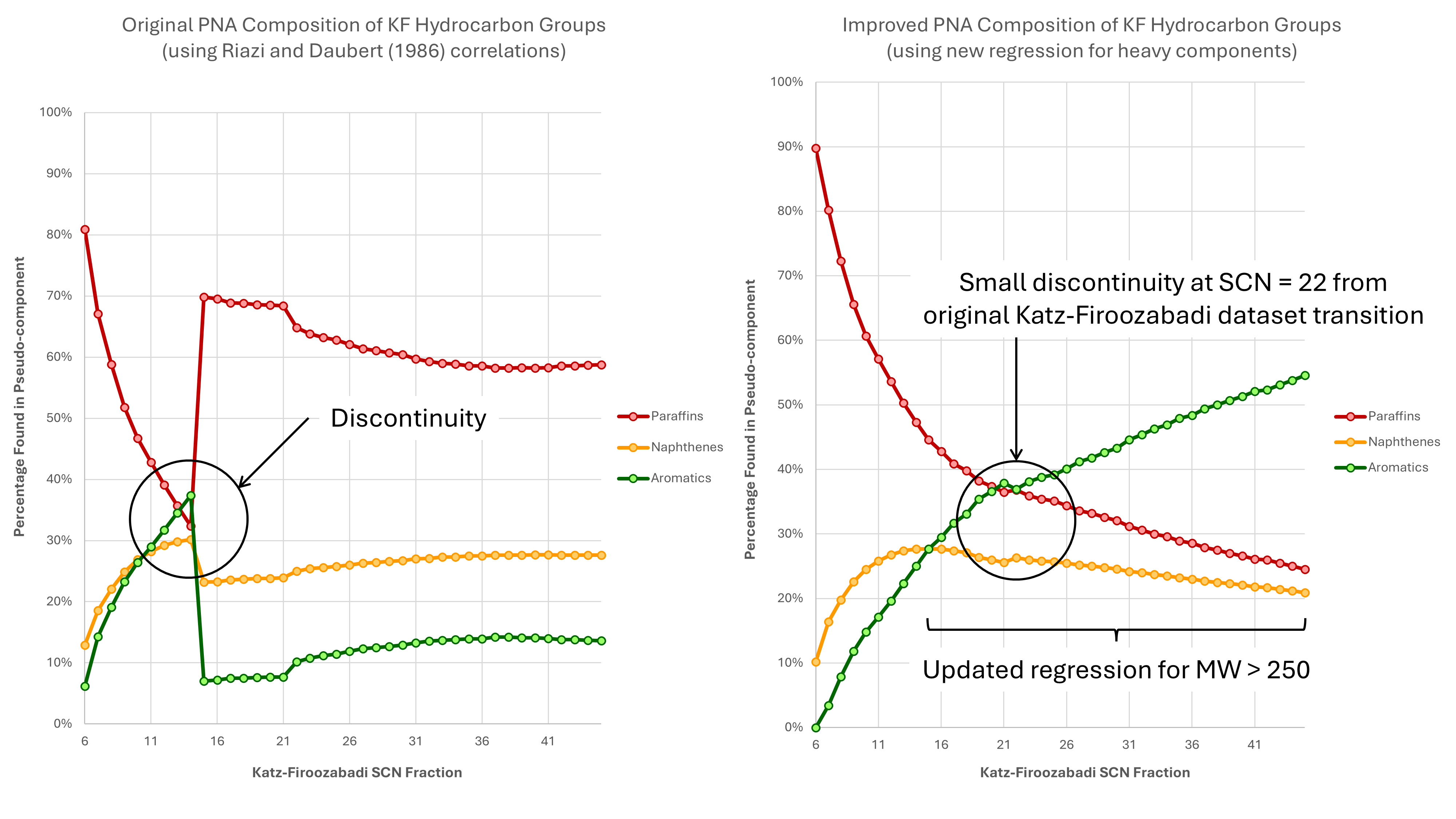
What is needed is a replacement correlation for the heavy fractions that is continuous with the light fractions. The results of a revised correlation are shown in the graph on the right in Figure 1. It can be seen that the discontinuity has been removed completely and the trends for paraffins, naphthenes and aromatics are continuous. A small discontinuity still remains at C21 to C22 which could be related to the underlying heavy fraction dataset used by Katz and Firoozabadi.
The methodology adopted to create this improved heavy fraction relationship is described in the following sections.
Method Outline
Firstly, I must give credit to Mark Burgoyne at Santos who was intrigued by my earlier blog post on C7+ characterisation, and took it upon himself to test out and adapt the methodology on some data he had available. The approach outlined here builds on and is inspired by his work.
- Assemble Pure Component Database: A database of known hydrocarbon types, including different paraffin, naphthene and aromatic molecules will be used to establish relationships between the different properties. The database will be used to establish relationships between the number of carbon atoms, the molecular weight and the specific gravity.
- Establish nC vs Tbp Relationships: A distillation cut is a narrow range of boiling points represented by an average boiling point. Within any distillation cut, a range of paraffins, naphthenes and aromatics will be present. The commonality between these different compounds is that they all share a similar average boiling point. The number of carbon atoms associated with a hydrocarbon type varies depending on the boiling point.
- Establish MW vs nC Relationships: If the number of carbon atoms is known for a PNA fraction, then it should be possible to predict the molecular weight.
- Establish SG vs nC Relationships: If the number of carbon atoms is known for a PNA fraction, then it should be possible to predict the specific gravity.
- Generate synthetic SCN fractions: Using the relationships that were established, a large synthetic dataset of distillation cuts covering the full range of single carbon numbers can be generated.
- Update Riazi-Daubert Heavy Fraction Regression: The heavy fraction relationships can be updated by least squares analysis of the new synthetic dataset.
Paraffin, Naphthene and Aromatic Database
There are many different arrangements of carbon and hydrogen atoms. A database containing properties for different paraffins, naphthenes and aromatic compounds has been used to model relationships. Because the database is not exhaustive, a mathematical approach that attempts to rigorously fit equations to the data has not been used. Instead the principle is to use the data to guide the modelled relationship, and tune the equations to match known results, such that the equations used do not violate the dataset.
Data for a total of 319 pure compounds was available and used to guide the modelled equations. The MW and SG for the different paraffins, naphthenes and aromatics are shown in Figure 2.
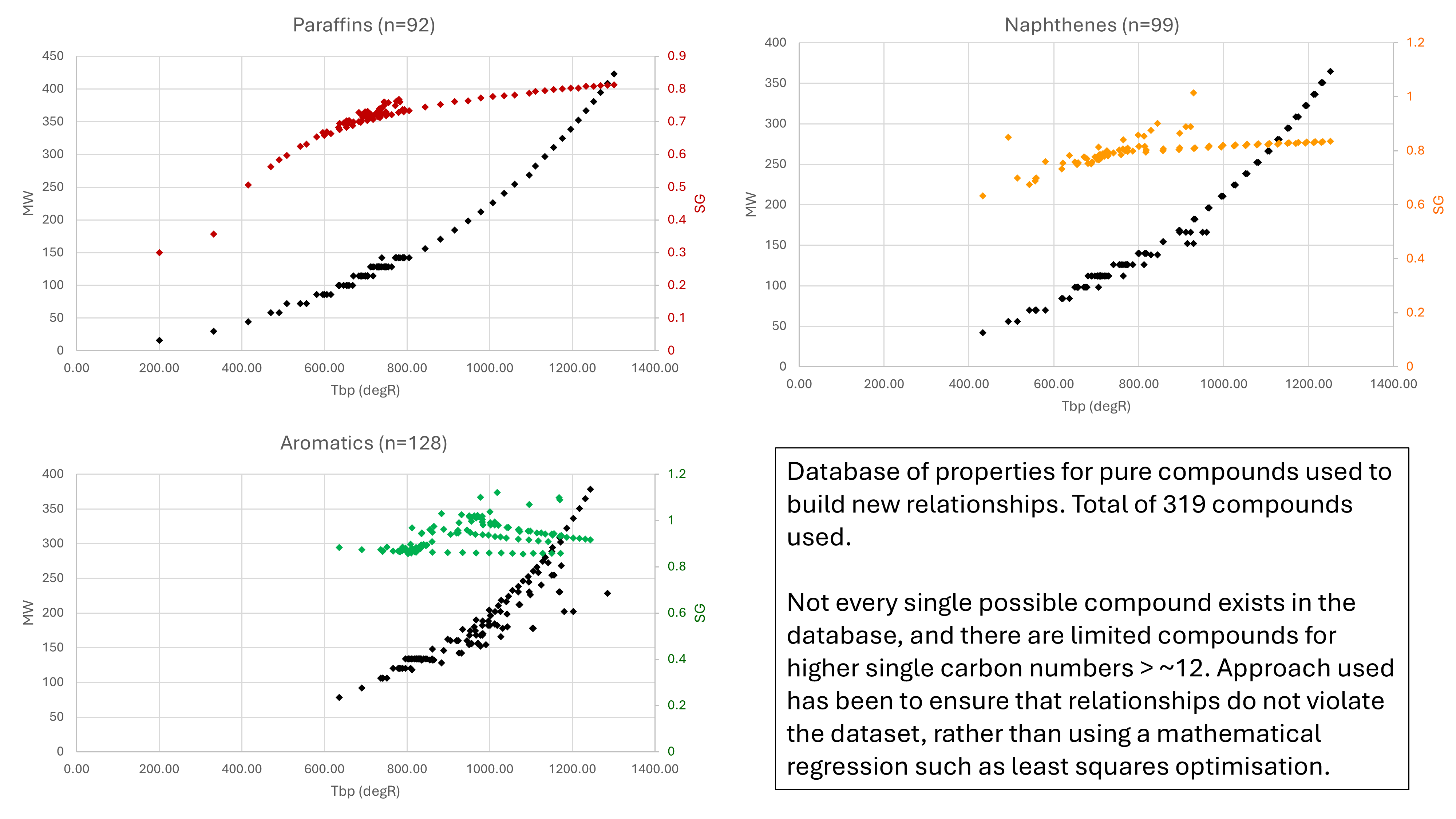
It is immediately evident that for all PNA fractions, there is scatter evident in the MW and SG that arises from the different combinations of molecules. Data for all PNA fractions to nearly 1,300 °R is available. This is equivalent to nearly 450 °C or a C30 SCN for normal paraffin.
Single Carbon Numbers
What exactly is the single carbon number (SCN), and what does it represent? I suspect that many petroleum engineers don’t give it too much thought as the answer is self-evident: “SCN is the number of carbon atoms associated with molecular compounds in a given petroleum fraction or pseudo-component”. When a laboratory analysis of a hydrocarbon mixture is analysed, most of the heavier compounds are grouped into single carbon number fractions. Closer examination of the report will also usually reveal that the properties of these fractions have been determined using Katz-Firoozabadi properties for single carbon number fractions.
These fractions are actually different distillation cuts from a true boiling point distillation analysis on a hydrocarbon sample. Each fraction contains molecular compounds with boiling points that fall into a narrow range around an average boiling point for that distillation cut. The molecular weights and densities associated with each fraction are measured. The boiling point for the normal paraffin that is closest to the average boiling point is said to be representative of the cut and the number of carbon atoms associated with that normal paraffin is used to describe the cut.
For example, consider the C10 cut. In the Katz-Firoozabadi data this is listed as a cut between 151.3 °C to 174.6 °C with an average boiling point of 165.8 °C (790.11 °R). In the updated recommended values of Riazi and Al-Sahhaf (1996) the boiling point is 440 K (792.0 °R). In comparison, the boiling point for the normal paraffin n-Decane is 805.15 °R (174.16 °C) which falls within the boiling point range. Hence this cut is designated with SCN = 10. However, other non-normal paraffins with 10 carbon atoms have lower boiling points such as 2,2,5,5-TetraMethylHexane at 739.1 °R (137.46 °C). Conversely, some Naphthenes and Aromatics with 10 carbon atoms have higher boiling points such as n-ButylCycloHexane at 817.37 °R (180.94 °C) and 1,2,3,4-TetraMethylBenzene at 860.74 °R (205.04 °C).
Figure 3 shows the datapoints for pure paraffins, naphthenes and aromatics plotted against their number of carbon atoms (nC).
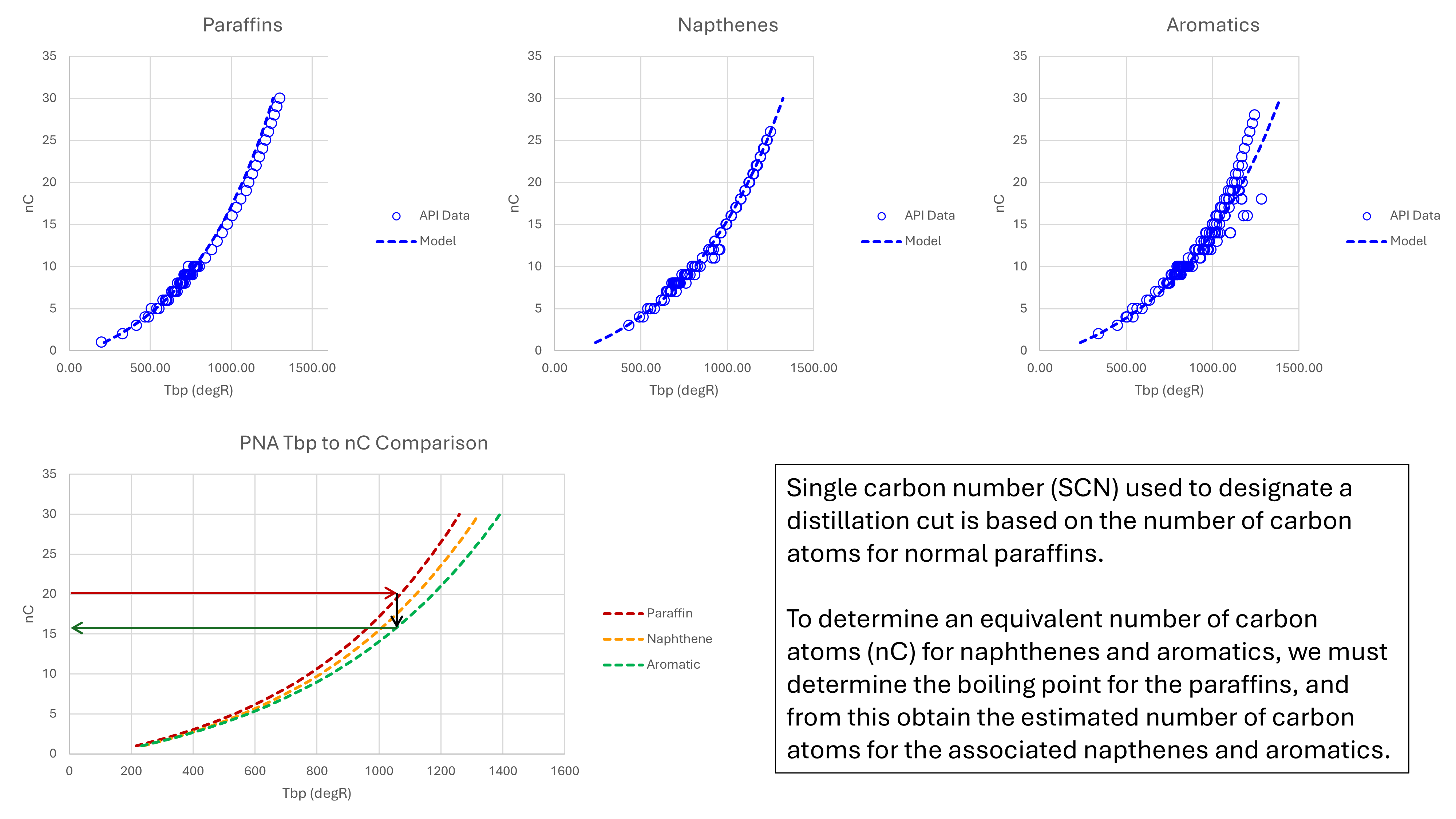
Although it is very tempting to fit a least squares regression to these data points, this is not recommended for the simple reason that the result would be biased to a particular subtype of each hydrocarbon type. For example, above 800 °R all the paraffins are normal paraffins and there is no representation from the non-normal paraffins. To ensure the influence of non-normal paraffins are captured, the model line appears to lie above the data points in this region. The model lines for naphthenes and aromatics are similarly chosen to reflect the average of all subtypes within a hydrocarbon type.
The equations for predicting boiling point in °C each are:
| Type | Equation |
|---|---|
| Paraffin | |
| Naphthene | |
| Aromatic |
These equations give rise to what Mark Burgoyne described as a ‘Rosetta Stone’ to convert between carbon numbers for different hydrocarbon types. For example if the average paraffin nC is known, then the equivalent aromatic nC can be determined by finding the intersection for a common true boiling point. An example of how this is achieved in Pyrus is shown in the code below:
import org.apache.commons.math3.analysis.UnivariateFunction;
import org.apache.commons.math3.analysis.solvers.BrentSolver;
public class PseudoComponent {
/**
* Estimate the single carbon number equivalence for this component. Multiplying the SCN by the group fractions will
* give the actual number of group components. This inverts the regressions for molecular weight versus the number
* of carbon atoms (nC) for paraffins, napthenes and aromatics using the API database.
*
* @param mass molecular mass in g/mole
* @param p paraffin fraction
* @param a aromatic fraction
* @return an equivalent single carbon number (nC) which is the average number of carbon atoms per molecule.
*/
public static double estimateCarbonNumber(double mass, double p, double a) {
double pcn = estimatePCN(mass, p, a);
double ncn = getNaphtheneCarbonNumFromPCN(pcn);
double acn = getAromaticCarbonNumFromPCN(pcn);
double n = 1.0 - p - a;
double scn_avg = p * pcn + n * ncn + a * acn;
return scn_avg;
}
/**
* Estimate the single carbon number equivalence for this component for the equivalent true boiling point cut.
*
* @param mass molecular mass in g/mole
* @param p paraffin fraction
* @param a aromatic fraction
* @return an equivalent paraffin carbon number (nC) which is the average number of carbon atoms per molecule.
*/
public static double estimatePCN(double mass, double p, double a) {
final double n = 1.0 - p - a;
UnivariateFunction f = (double nc_p) -> {
double mw = estimateMass(nc_p, p, n, a);
return mass - mw;
};
BrentSolver solver = new BrentSolver(1.0e-06);
double guess = estimateCarbonNumberSimple(mass, p, a);
double pcn = solver.solve(100, f, guess / 2.0, guess * 2.0, guess);
return pcn;
}
/**
* Estimate the single carbon number equivalence for this component. Multiplying the SCN by the group fractions will
* give the actual number of group components. This is done by looking at the molecular weight and working from an
* assumption that formulae for paraffins are C.n H.2n+2, naphthenes are C.n H.2n and aromatics are C.n H.2n-6. For
* example n-Decane is C10H22, n-Pentylcyclopentane is C10H20 and n-Butylbenzene is C10H14.
*
* @see #estimateCarbonNumber(double, double, double)
* @param mass molecular mass in g/mole
* @param p paraffin fraction
* @param a aromatic fraction
* @return an equivalent single carbon number
*/
public static double estimateCarbonNumberSimple(double mass, double p, double a) {
double scn_equiv = (mass - 1.00794 * (2.0 * p - 6.0 * a)) / (12.011 + 2.0 * 1.00794);
return scn_equiv;
}
/**
* As described by Mark Burgoyne, this is a 'Rosetta Stone' approach to convert a distillation cut SCN (which is
* typically the paraffin nC) into an equivalent naphthene carbon number that would be present in that cut. For a
* given boiling point, the number of carbon atoms associated with the naphthenes is less than the SCN for the
* paraffins.
*
* @param pcn paraffin carbon number for the distillation cut
* @return the equivalent carbon number for the naphthenes in this cut
*/
public static double getNaphtheneCarbonNumFromPCN(double pcn) {
double tbp_degc = getTbpFromPCN(pcn);
double ncn = exp((tbp_degc + 700.0) / 328.0) - 4.5;
return ncn;
}
/**
* As described by Mark Burgoyne, this is a 'Rosetta Stone' approach to convert a distillation cut SCN (which is
* typically the paraffin nC) into an equivalent aromatic carbon number that would be present in that cut. For a
* given boiling point, the number of carbon atoms associated with the aromatics is less than the SCN for the
* paraffins.
*
* @param pcn paraffin carbon number for the distillation cut
* @return the equivalent carbon number for the aromatics in this cut
*/
public static double getAromaticCarbonNumFromPCN(double pcn) {
double tbp_degc = getTbpFromPCN(pcn);
double acn = exp((tbp_degc + 740.0) / 350.0) - 4.5;
return acn;
}
/**
* Predicted boiling point for a typical paraffin based on the number of carbon atoms. Note that this is the boiling
* point for an average of normal and non-normal paraffins. Therefore it will not match the boiling points for
* normal paraffins that are typically reported (for a given number of carbon atoms it will be lower).
*
* @param pcn paraffin carbon number for the distillation cut
* @return boiling point in degrees Celsius
*/
protected static double getTbpFromPCN(double pcn) {
return 305.0 * log(pcn + 4.1) - 650.0;
}
}
Predicted Properties from Number of Carbon Atoms
Instead of plotting MW and SG against true boiling point, we can plot these parameters against the number of carbon atoms for each hydrocarbon type. Instead of plotting SG, the parameter nC/SG is plotted which yields an approximately linear trend.
For the MW vs nC trends, a linear regression is used. The relationships obtained appear consistent with calculation of the molecular weight from first principles. For example, a normal paraffin with n carbon atoms should have 2 × n + 2 hydrogen atoms. Given a carbon MW of 12.011 g/mol and a hydrogen MW of 1.00794 g/mol, this would give an exact MW of n × (12.011 + 2 × 1.00794) + 2 × 1.00794 g/mol = 14.02688 × n + 2.01588 g/mol. This is the same equation that emerges from the linear regression.
The nC/SG vs nC trends are manual fits to the data points. The fits have been chosen so that they don’t violate any data. The final PNA results obtained are sensitive to these equations, and so they have been tuned by fitting the predicted PNA fractions for Volve to the measured fractions. It should be noted that there is no unique and perfect solution. By tuning these relationships we achieve a ‘good enough’ relationship that allows a practical prediction of PNA for our distillation cuts.
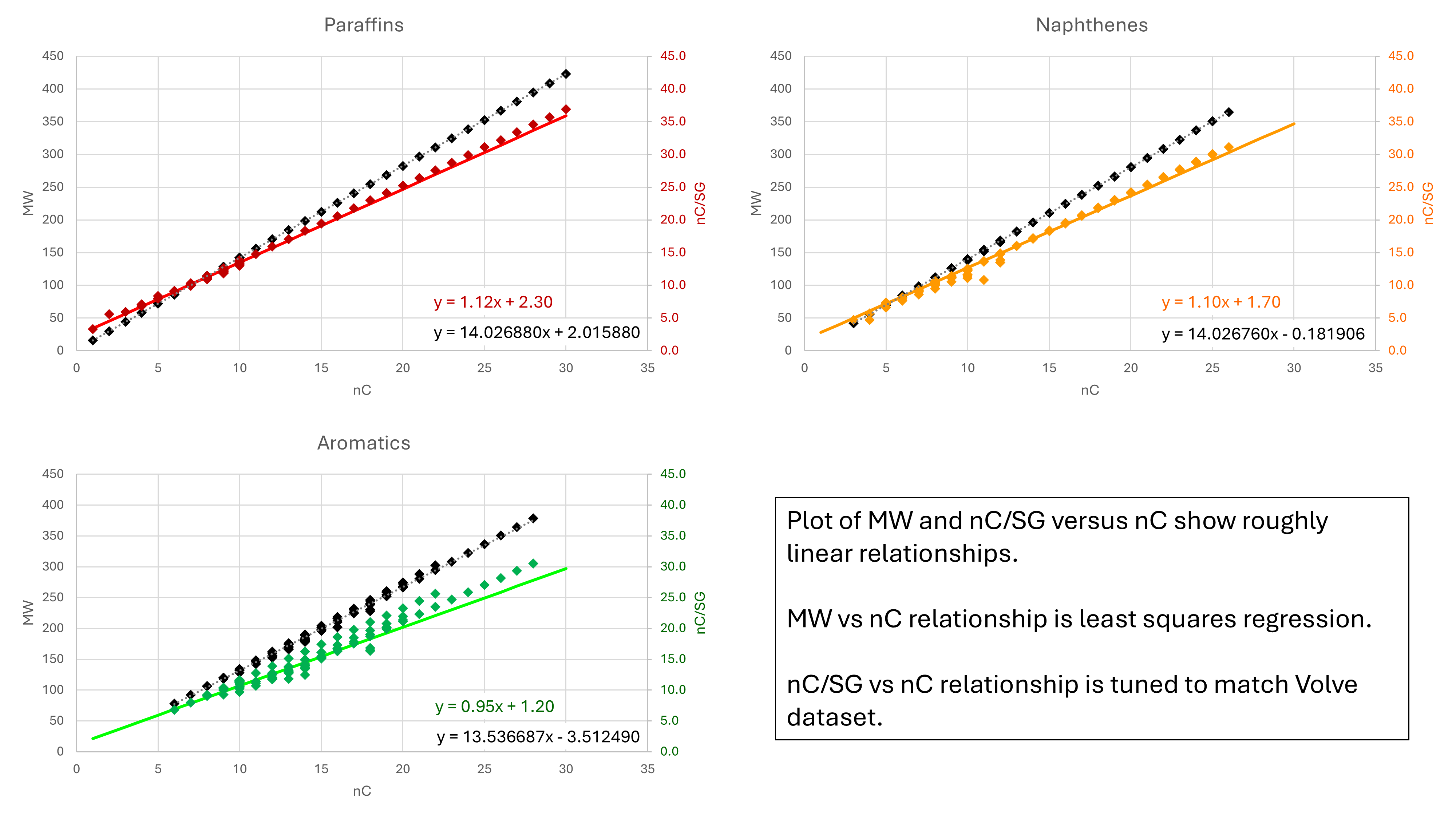
We can estimate the molecular weight and specific gravity for a fraction based on the paraffin carbon number as follows:
/**
* Determine the molecular mass from the equivalent single carbon number and the PNA fractions. For any given single
* carbon number, the ratio of carbon and hydrogen atoms is determines by the molecular structure. Therefore this
* method will return a mass that is closely tied to the typical molecular structures that are found for paraffins,
* naphthenes and aromatics. The equations are simple linear regressions against all paraffins, napthenes and
* aromatics in the API database. Thus they account for poly-aromatics.
*
* @param pcn paraffin carbon number
* @param p proportion of pseudo-component comprising straight chain or branched paraffins
* @param n proportion of pseudo-component comprising cyclic (saturated) ring as major structure
* @param a proportion of pseudo-component comprising aromatic (single ring)
* @return the estimated molecular weight in g/mole or lbm/lbm-mol
*/
public static double estimateMass(double pcn, double p, double n, double a) {
double ncn = getNaphtheneCarbonNumFromPCN(pcn);
double acn = getAromaticCarbonNumFromPCN(pcn);
return p * getParaffinMassFromCarbonNum(pcn) + n * getNaphtheneMassFromCarbonNum(ncn)
+ a * getAromaticMassFromCarbonNum(acn);
}
/**
* Estimates the specific gravity from the paraffin carbon number and the PNA composition of the component.
*
* @param pcn paraffin carbon number
* @param p proportion of pseudo-component comprising straight chain or branched paraffins
* @param n proportion of pseudo-component comprising cyclic (saturated) ring as major structure
* @param a proportion of pseudo-component comprising aromatic (single ring)
* @return the specific gravity for this single carbon number
*/
public static double estimateGamma(double pcn, double p, double n, double a) {
double ncn = getNaphtheneCarbonNumFromPCN(pcn);
double acn = getAromaticCarbonNumFromPCN(pcn);
double mw_p = getParaffinMassFromCarbonNum(pcn);
double mw_n = getNaphtheneMassFromCarbonNum(ncn);
double mw_a = getAromaticMassFromCarbonNum(acn);
double sg_p = getParaffinSgFromCarbonNum(pcn);
double sg_n = getNaphtheneSgFromCarbonNum(ncn);
double sg_a = getAromaticSgFromCarbonNum(acn);
// Work out the mixure properties. Use molar fractions for mass and calorific value, and weight fractions for
// specific gravity.
double mw_tot = p * mw_p + n * mw_n + a * mw_a; // molecular mass
double gamma = 0.0;
double wtfrac_p = p * mw_p / mw_tot;
gamma += wtfrac_p / sg_p;
double wtfrac_n = n * mw_n / mw_tot;
gamma += wtfrac_n / sg_n;
double wtfrac_a = a * mw_a / mw_tot;
gamma += wtfrac_a / sg_a;
return 1.0 / gamma;
}
/**
* Mass of paraffinic components from true average number of carbon atoms.
*
* @param pcn average number of carbon atoms
* @return molecular weight of paraffinic components
*/
public static double getParaffinMassFromCarbonNum(double pcn) {
return 14.02688 * pcn + 2.01588;
}
/**
* Mass of naphthenic components from true average number of carbon atoms.
*
* @param ncn average number of carbon atoms
* @return molecular weight of naphthenic components
*/
public static double getNaphtheneMassFromCarbonNum(double ncn) {
return 14.02676 * ncn - 0.1819064;
}
/**
* Mass of aromatic components from true average number of carbon atoms.
*
* @param acn average number of carbon atoms
* @return molecular weight of aromatic components
*/
public static double getAromaticMassFromCarbonNum(double acn) {
return 13.536687 * acn - 3.51249;
}
/**
* Specific gravity of paraffinic components from true average number of carbon atoms.
*
* @param pcn average number of carbon atoms
* @return specific gravity of paraffinic components
*/
public static double getParaffinSgFromCarbonNum(double pcn) {
double nc_over_sg = 1.12 * pcn + 2.3; // simplified trendline tuned to produce better behaviour
return pcn / nc_over_sg;
}
/**
* Specific gravity of naphthenic components from true average number of carbon atoms.
*
* @param ncn average number of carbon atoms
* @return specific gravity of naphthenic components
*/
public static double getNaphtheneSgFromCarbonNum(double ncn) {
double nc_over_sg = 1.1 * ncn + 1.7; // simplified trendline tuned to produce better behaviour
return ncn / nc_over_sg;
}
/**
* Specific gravity of aromatic components from true average number of carbon atoms.
*
* @param acn average number of carbon atoms
* @return specific gravity of aromatic components
*/
public static double getAromaticSgFromCarbonNum(double acn) {
double nc_over_sg = 0.95 * acn + 1.2; // simplified trendline tuned to produce better behaviour
return acn / nc_over_sg;
}
Creating Synthetic Distillation Cuts
We now have a complete system to relate MW, SG, SCN and PNA. We can generate a synthetic dataset of distillation cuts with random amounts of paraffin, naphthene and aromatic content. Rather than just generating completely random fractions, we attempt to honour the observation that fractions typically get more aromatic and less paraffinic as the single carbon number and true boiling point increases.
A typical relationship is shown in Figure 5. The trends on this chart are used to determine ranges for the paraffin and aromatic content, with naphthene being n = 1.0 - p - a. The ranges are tabulated for C6 through to C40 in Figure 5.
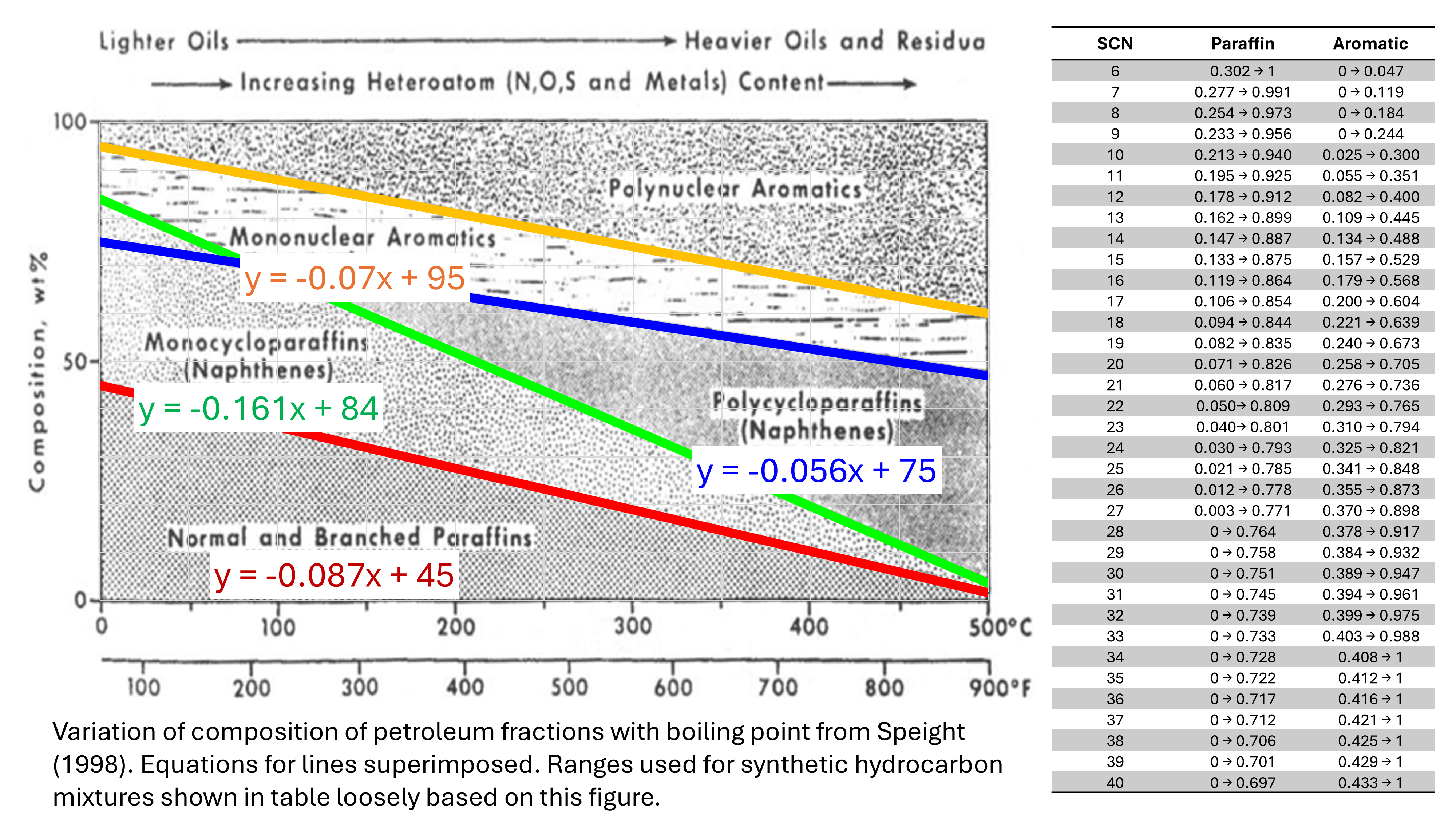
The dataset generated has 100 random synthetic cuts for paraffin carbon numbers from 6 through to 45, for a total of 4,000 synthetic cuts in total.
Updated Riazi-Daubert Regressions for Heavy Fraction
The existing Riazi-Daubert equations for heavy fractions (MW > 200) uses the refractivity intercept (RI) and the carbon-hydrogen weight ratio (CH). A multi-variate regression to model paraffin fraction and aromatic fraction from these parameters has been performed using the synthetic dataset. The revised equations are shown as the ‘Heavy Paraffin’ and ‘Heavy Aromatic’.
This revised equation has a small discontinuity with the original light fraction equations of Riazi and Daubert. To ensure a continuous function, the gamma co-efficient in the original equation has been very slightly tweaked so that the light and heavy equations are continuous.
| Type | Original Equation | Revised Equation |
|---|---|---|
| Light Paraffin | ||
| Light Naphthene | ||
| Heavy Paraffin | ||
| Heavy Naphthene | – | |
| Heavy Aromatic | – |
Java code to implement these equations is given in a post on C7+ characterisation. It should be trivial to adapt that code which uses the original relationships to the new ones.
Model Tuning
As mentioned previously, the equations used to predict MW and SG from nC for the different PNA hydrocarbon types have been tuned to match the measured results for the Volve dataset. This is shown in the lower chart of Figure 6. Adjusting these relationships has the effect of moving the predicted paraffin, naphthene and aromatic lines up or down. The general relative trends in terms of increasing aromatic content and decreasing paraffin content with higher SCN are unchanged by tuning the relationships.
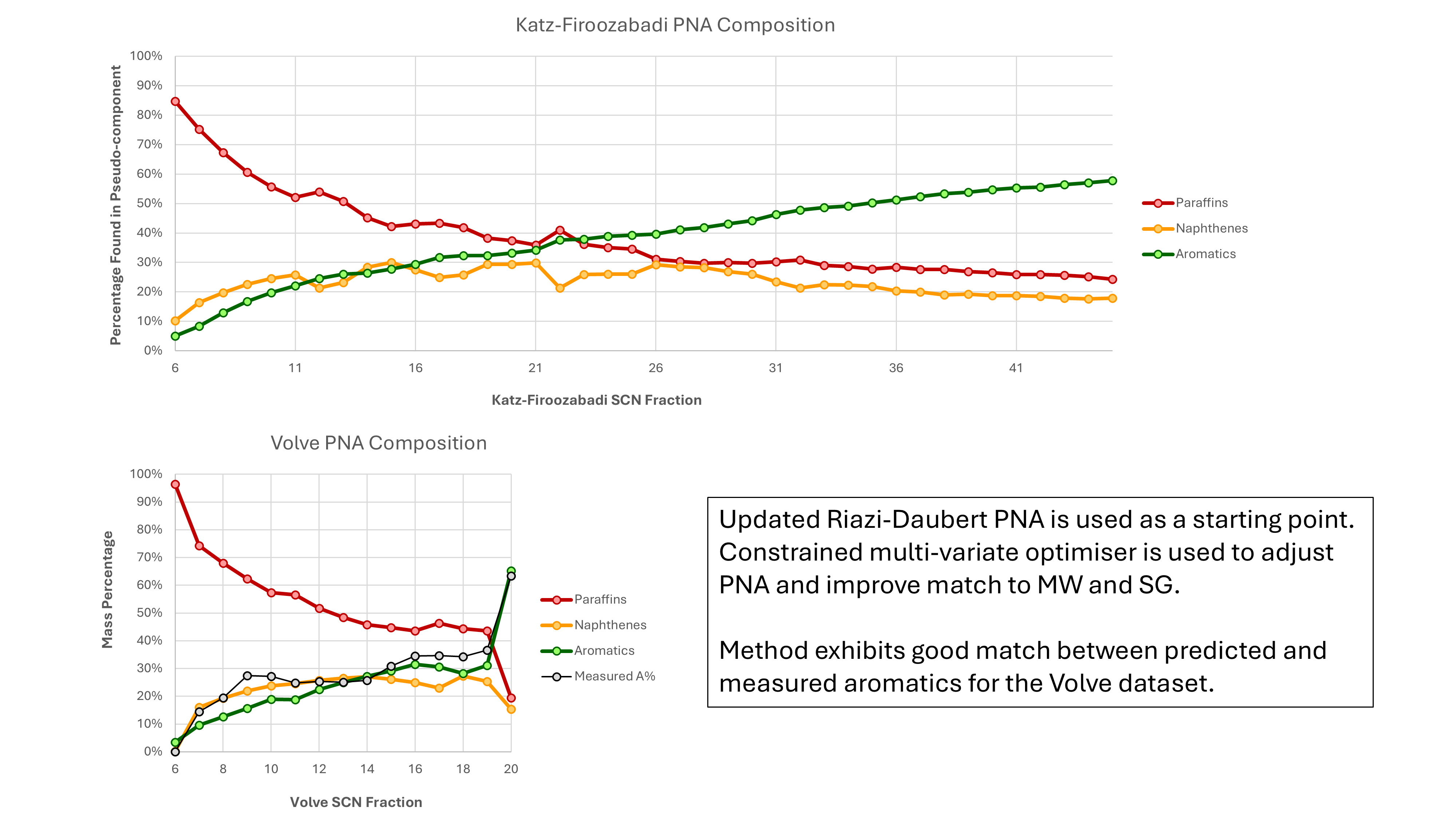
The final step is to optimise the PNA so that the MW and SG associated with the SCN and PNA match exactly. The approach used is to use a constrained multi-variate optimiser to minimise the error in an objective function given by abs(mw_calc - mass) / mass + abs(sg_calc - gamma) / gamma where mass is the target molecular weight and gamma is the target specific gravity. An optimiser from the Apache Commons Math library has been used to avoid re-inventing the wheel. It appears to work well enough.
Note that there are often multiple solutions that can be found. The approach used has been the restrict the PNA values to remain within a narrow band around the updated Riazi-Daubert modelled PNA fractions.
How well does this work?
Let’s look at the C15 fraction which was the first SCN after the discontinuity encountered in the previous analysis. Recall earlier we discussed the recommended values of Riazi and Al-Sahhaf (1996). This paper shows that for the C15 cut the boiling point is 539 K (970.2 °R or 265.85 °C). The associated MW is 207 and the SG is 0.836.
Our methods discussed in this post predict P% = 42.3%, N% = 30.0 and A% = 27.7%. The SCN for this cut is calculated as 14.899 which is very close to 15, and is the average of the paraffin carbon number (16.159), naphthene carbon number (14.608) and the aromatic carbon number (13.295). Given that the PCN is higher than 15, a valid concern might be that the true boiling point for this cut doesn’t match the data. However, the PCN used includes normal and non-normal paraffins. The Tbp for this modelled cut is 267.6 °C which is close to the expected value. Similarly the MW is 207 versus an expected value of 207, and the SG is 0.836 versus an expected value of 0.836.
Overall this is a very good match. Similar results are obtained for all Katz-Firoozabadi fractions from C6 through to C45. The only fractions where a perfect match is not obtained are with the lighter fractions C10 and lower, where the specific gravity is up to 3% lower. It is very likely that this is because of the constraint imposed on the optimiser which restricts the amount of aromatic content that can be included (and which would allow a better match to the SG).
import org.apache.commons.math3.analysis.MultivariateFunction;
import org.apache.commons.math3.optim.InitialGuess;
import org.apache.commons.math3.optim.MaxEval;
import org.apache.commons.math3.optim.PointValuePair;
import org.apache.commons.math3.optim.SimpleBounds;
import org.apache.commons.math3.optim.nonlinear.scalar.GoalType;
import org.apache.commons.math3.optim.nonlinear.scalar.MultivariateOptimizer;
import org.apache.commons.math3.optim.nonlinear.scalar.ObjectiveFunction;
import org.apache.commons.math3.optim.nonlinear.scalar.noderiv.BOBYQAOptimizer;
public class PseudoComponent {
/**
* Optimises the PNA to fit a given molecular weight and specific gravity for a distillation cut. The method
* searches for the PNA fractions that match by first determining the carbon number for paraffin (PCN) that allows a
* match to the molecular weight. Naphthene carbon number and aromatic carbon number used for calculating the
* molecular weight are derived from the PCN via a consistent true boiling point. Once the PCN is determined the
* specific gravity can also be calculated. The objective function seeks to minimise the error between the target
* molecular weight and specific gravity. Method assumes that main characterisation parameters such as molecular
* weight, normal boiling point and specific gravity have already been set.
*
* @param mass the component mass in g/mole
* @param gamma the component specific gravity
* @return PNA characterisation fractions [p, n, a, pa, ma] where p is paraffin, n is naphthene, a is aromatic, pa
* is polyaromatic and ma is monoaromatic. Note p + n + a = 1.0 and pa + ma = a.
*/
public static double[] estimatePNA(double mass, double gamma) {
// Initial starting guess for PNA fraction from Riazi-Daubert
final double[] start_pna = estimateRiaziDaubertPNA(mass, gamma);
// Objective function to minimise difference between target mass and gamma, and the calculated value for the
// current PNA fractions.
MultivariateFunction function = (double[] pa) -> {
double p = pa[0];
double a = pa[1];
// Impossible if more than 100% paraffin and aromatic
if (p + a > 1.0) {
return 1.0e12;
}
double n = 1.0 - p - a;
double pcn = estimatePCN(mass, p, a);
double mw_calc = estimateMass(pcn, p, n, a);
double sg_calc = estimateGamma(pcn, p, n, a);
final double obj_func = (abs(mw_calc - mass) / mass + abs(sg_calc - gamma) / gamma);
return obj_func;
};
// Set up a non-linear multivariate constrained optimiser to search for the solution.
MultivariateOptimizer optimizer = new BOBYQAOptimizer(5);
PointValuePair result = optimizer.optimize(
new MaxEval(200),
GoalType.MINIMIZE,
new InitialGuess(new double[]{start_pna[0], start_pna[2]}),
new ObjectiveFunction(function),
new SimpleBounds(
new double[]{max(0.0, start_pna[0] - 0.05), max(0.0, start_pna[2] - 0.05)},
new double[]{min(1.0, start_pna[0] + 0.05), min(1.0, start_pna[2] + 0.05)}));
double p = result.getPoint()[0];
double a = result.getPoint()[1];
double n = 1.0 - p - a;
double[] aro_split = getAromaticSplit(a, mass, gamma);
final double[] optim_pna = new double[]{p, n, a, aro_split[0], aro_split[1]};
return optim_pna;
}
}
References
- Riazi, M. R. and Al-Sahhaf, T. A. 1996. Physical Properties of Heavy Petroleum Fractions and Crude Oils. Fluid Phase Equilibria 117 (1-2): 217-224. https://doi.org/10.1016/0378-3812(95)02956-7
- Speight, J. G. 1998. The Chemistry and Technology of Petroleum, third edition. New York: Marcel Dekker.